矩阵代数分解

按课程顺序，讲矩阵分解之前是将矩阵分解。

分析：确定量的特征值的坐标系

分解：矩阵分解 (decomposition, factorization)是将矩阵拆解为数个矩阵的乘积，可分为三角分解、满秩分解、QR分解、Jordan分解和SVD（奇异值）分解等。

几种分解

初等变换 (任意)

方阵 A 与 B 等价的充要条件是存在 m 阶可逆矩阵 P 及 n 阶可逆矩阵 Q ，使 PAQ = B .（差不多就这定理的意思）

三角分解 (任意）

$$PA=LU$$

白话：矩阵A换行以后，可以表示为下三角乘上三角矩阵

matlab： [L,U,P] = lu(A)

Cholesky分解(乔里斯基) (实对称正定方阵）

$$A=LL^T$$

• L为非奇异下三角矩阵。
• 若限定L的对角元素为正，则这种分解是唯一的.

matlab：chol(A)

C.Schur分解 (方阵)

$$A=PRP^T$$

P为酉矩阵，R为对角线为特征值的上三角矩阵

matlab: [P,R]=schur(X)

​ 因为X的特征值有实数解和复数解，所以有

• schur(X,’real’)
• schur(X,’complex’)

QR分解 （列向量线性无关窄方矩阵）

$$A=QP$$

Q为酉矩阵，R为上三角矩阵

matlab：[Q,P]=qr(A)

​ [Q,P]=qr(A,0) (貌似用来去0行的？)

对角化 (方阵，特征向量有要求n个无关)

一种相似变换（特征值相同的矩阵）

$$A \vec{x}=\lambda \vec{x}$$ $$A=V\sum V^{-1}$$

• 特征值： $\lambda$

• 特征向量：非零向量$\vec{x}$

• 特征值的代数多重度：有几重根

• 特征值的几何多重度：有几个特征向量

  有几何多重度<=代数多重度，n重根可能解出n-1个或者n-2个···特征向量，不恰当的例子)

matlab：[V,D]=eig(A) V为特征向量 D特征值

性质:根据基础解系就知道是线性无关的一些性质了

对角分解的推导：

$$对于特征向量u_1,有Au_1=\lambda_1 u_1$$ $$同理有Au_2=\lambda_2 u_2$$ $$有A[u_1,u_2···,u_n]=[\lambda_1 u_1,\lambda_2 u_2···,\lambda_n u_n]$$ $$即AV=V\sum$$

注意到V是要求逆的，因此规定特征向量要有n个线性无关的，这样的矩阵才能进行对角分解

特征值分解

只适用于hermitian矩阵

$$A=V\sum V^{T}$$

Jordan标准型 （方阵）

矩阵的条件数：矩阵或系数对解向量的影响

特征值的条件数：矩阵扰动对特征值对影响

谱：所有特征值的集合

谱半径：$max(\lambda)$

谱分解：

$$A=PJP^{-1}$$

• 特征值分解是其的一种特殊形式
• J块个数等于几何多重度，J块总大小等于代数多重度
• 每块大小服从：（貌似知道3阶4阶就行）

• J块形式

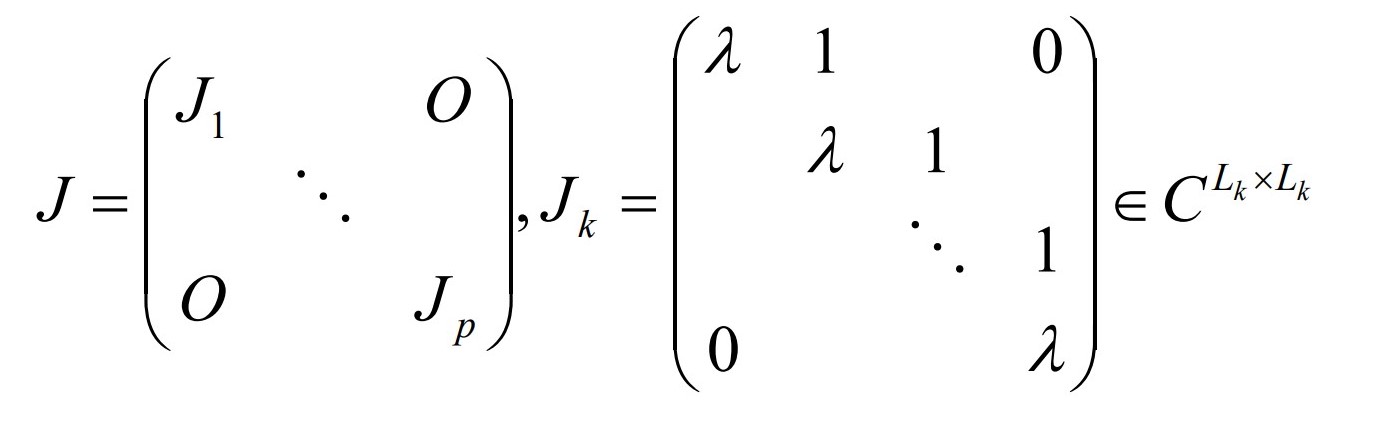
应用

基于特征值分解的图像压缩

保留最大的一部分特征值对应的特征向量

主成分分析PCA

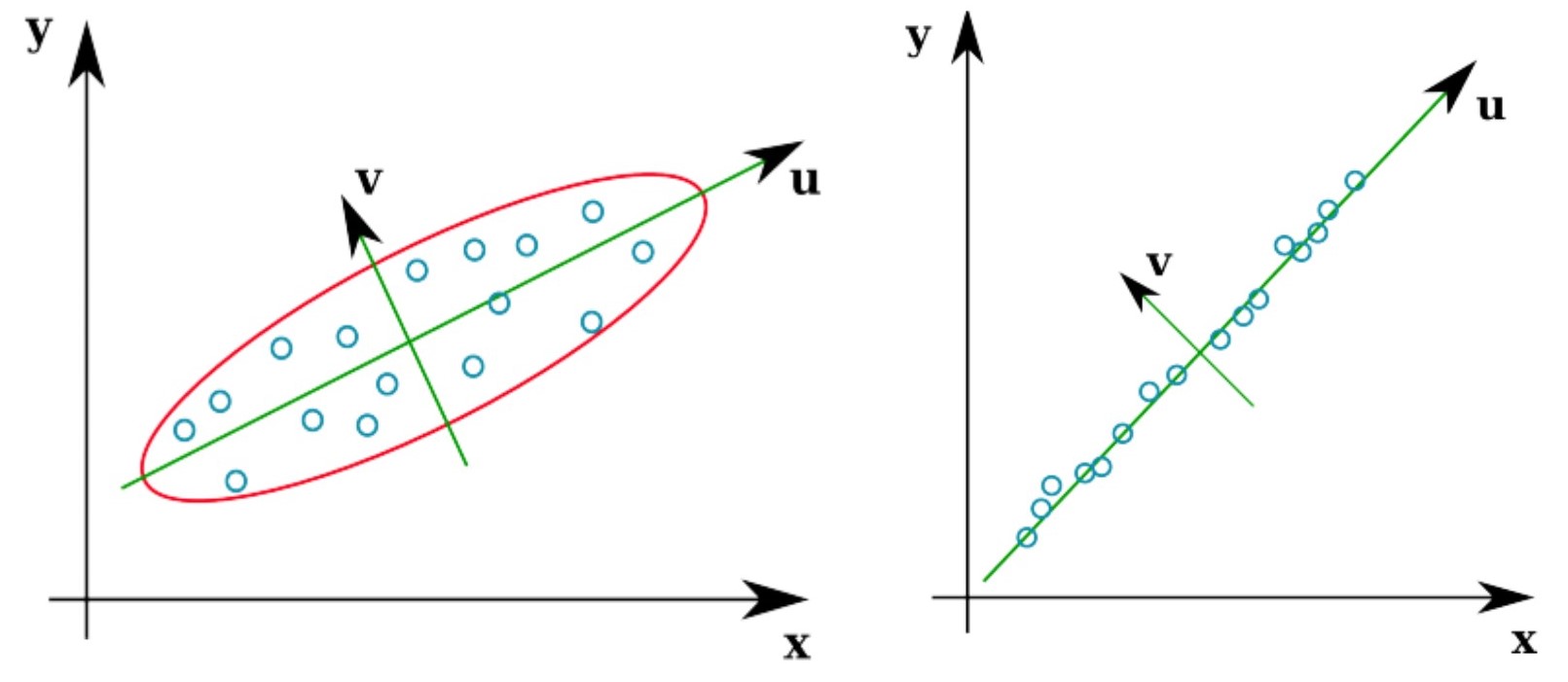
如图，数据有两个特征值，保留最大的那个。

Kenrnel PCA

因为普通PCA只能线性变换，对于一些数据可以用kernel PCA做非线性变换。

角点检测

看图像沿不同维度变化的大小

光流估计

运动跟踪？

广义特征值分解

$$Ax=\lambda Bx$$